【数学小話】本当に同じ距離なのか？
↓ここからカテゴリー別に記事を見ることができます。↓
問題提起
数学の問題で見かける、京都の街並みのように碁盤状に走る道を歩く状況設定。
AからBへ行く道は、右と上にのみ進むことを考えると、どのルートであっても最短距離となる。これは数学の問題でよく見ることです。
(右右上上上右右と進んでも、右右右右上上上と進んでも距離は同じ)
実生活においても、このような道を歩く時は本当にどのルートであっても同じ距離となるのでしょうか？
筆者は散歩をしながら時折この問題を思い出しては、定量的な考察は頭の中だけで計算量しきれないと思い断念していましたが、ここで長年の問題に決着をつけたいと思います。
なぜ実生活では違う距離だと疑うのか、それは数学と実生活における一番の違いである、道の幅の存在です。
数学では直線は幅を持たないものとして扱われますが、現実の道は幅があります。
モデル化
では、簡単な例として、下のような、AとB2つの道を考え、それぞれのルートの最短距離を求めてみましょう。
Aルートは1回のみ直角に曲がる道で、Bルートは3回直角に曲がる道です。
数学とは違い、現実の道には幅があります。また、計算のしやすさを考慮して、スタート地点とゴール地点をすこし動かし、今回はコーナーをギリギリで攻める、以下のようなルートをとりましょう。ついでに、道の距離や幅を文字で置きましょう。
縦の長さを2a、横の長さを2b、道幅をmとしました。なぜ2a、2bとしたかというと、Bルートが同じ歩き方を2回繰り返すようなルートだからです。
計算
さて、Aルート、Bルートの距離を求めるのに使う道具は三平方の定理です。中学3年生で習います。
1つ目の式が、三平方の定理の式です。直角三角形の三辺の長さに関する公式です。
では、さっそく道のりを求めていきます。下のように紫の直角三角形を作ります。
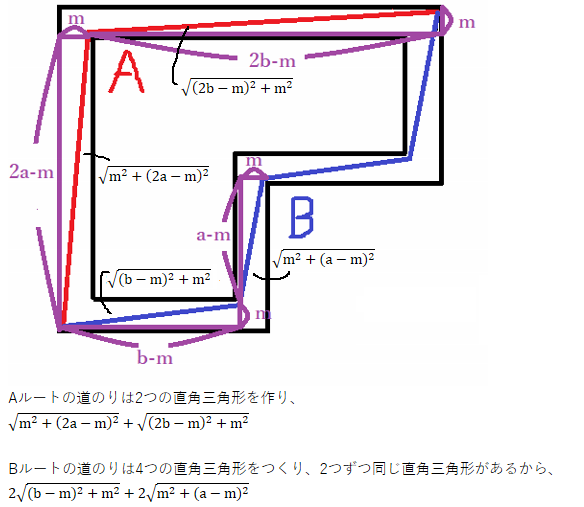
あとは、これらのどちらが大きいかを判断するだけです。 どちらが大きいか判断するには、差をとるのが手っ取り早いです。
AとBのどちらが大きいか知りたいとき、A-Bを計算します。A-B>0ならA>B、A-B<0ならA<Bという至極当然のことを用いるわけです。
今回は、根号が含まれているものの大小を知りたいので、それぞれを2乗してから差をとります。それぞれを2乗しても大小関係は変わりません。
以上の計算より、a,bがmの3/2倍以上の時、Aルートの方が大きいということが分かりました。普段の道路において、a,bがどこを表す文字かを考えると、a,bはmの3/2倍以上であるのは当然としてよいでしょう。
よって、縦の道も横の道も、AルートよりBルートの方が短いということが分かりました。
結論
なるべく多く直角に折れ曲がる道を選(んでコーナーのギリギリを攻めるように進)んだ方が最短距離は短くなる
考察
現実に存在する道路には、ここで考えたモデルよりはるかに折れ曲がる回数が増えたものや、折れ曲がる角度が90度でない道路などがたくさんあります。今回の非常に単純な道路モデルの比較結果から、より多く折れ曲がる道の方が最短距離が短いという法則はおそらくどこでも成り立つと予想できます。それが本当かどうかを確かめるのは皆さんにお任せします。
この記事の冒頭で示した碁盤状に走る道でAからBへ進むとき、道の幅を考える現実世界においては、このような赤の矢印の通りに、コーナーのギリギリを攻めるように進むのが一番近いです。
今回、このような問題を考えながら、日常のちょっとした疑問や課題を解決するために数学が役立つよい一例だなと思いました。
これから道を歩くときはなるべく(直角に)多く曲がる道を、コーナーのギリギリをつくように歩いていきたいと思います。
written by k
Copyright © 2017 日比谷高校のススメ All rights reserved.
