【数学小話】ほんとうに0.999...=1なのか② 本当の説明

前回はこちら

【数学小話】ほんとうに0.999...=1なのか① 1/3を使う証明は間違い？

0.999...=1

これがなぜ正しいのか、そもそもこの式の意味は何なのか、ということを説明するという目的のこのシリーズ。前回は中学生向けとしてよく見られる証明を紹介しました。今回は、高校の理系レベルの数学に触れつつ、この式の適切な説明、解釈を話します。

極限

極限というのは、高校３年理系が習う数IIIに登場する単元です。記号の意味を理解すれば、中学生でも十分今回の話は理解可能です。

極限は、一言で言うと、「限りなくこうなる」というものです。

 

このように数を並べていくと、登場する数はどんどん小さくなっていきます。また、分母も分子も常に正ですから、登場する数はどこまでいっても負になりえません。

ここに登場する値は、先にいけばいくほど、値が限りなく0に近づくことは直感でわかると思います。その0に近づくということを例えばこのように書きます。

この式の意味は、nの値を正の無限大に持っていくと、の値は限りなく0に近づいていく、ということです。limは「リミット」と読み、極限を表す記号です。

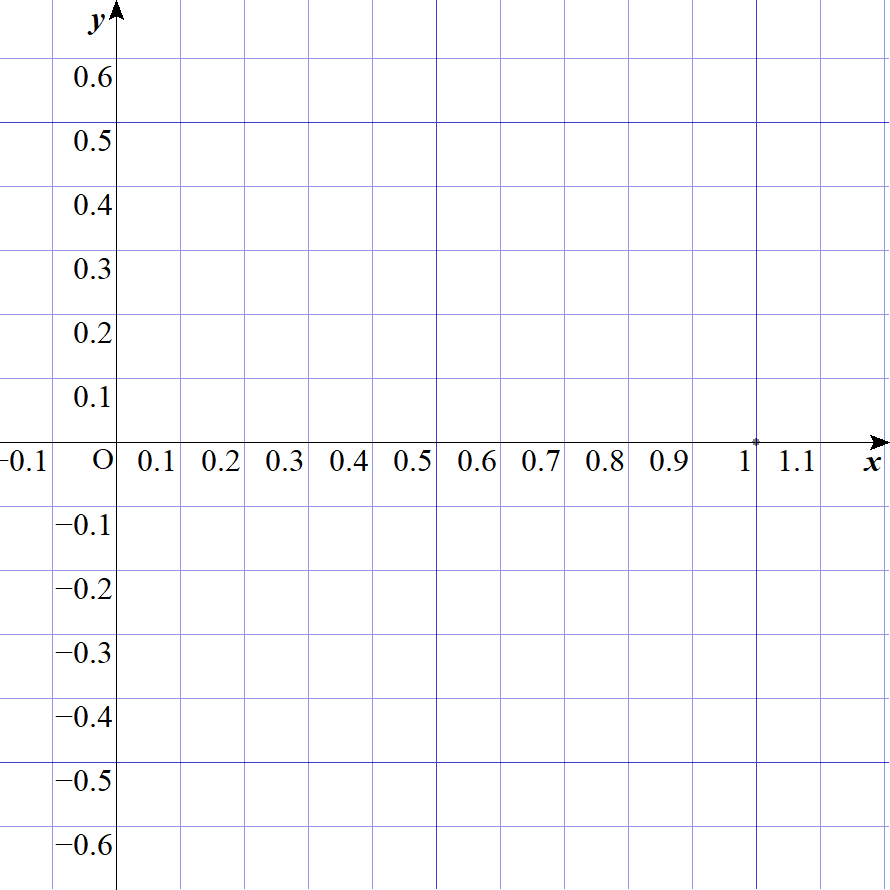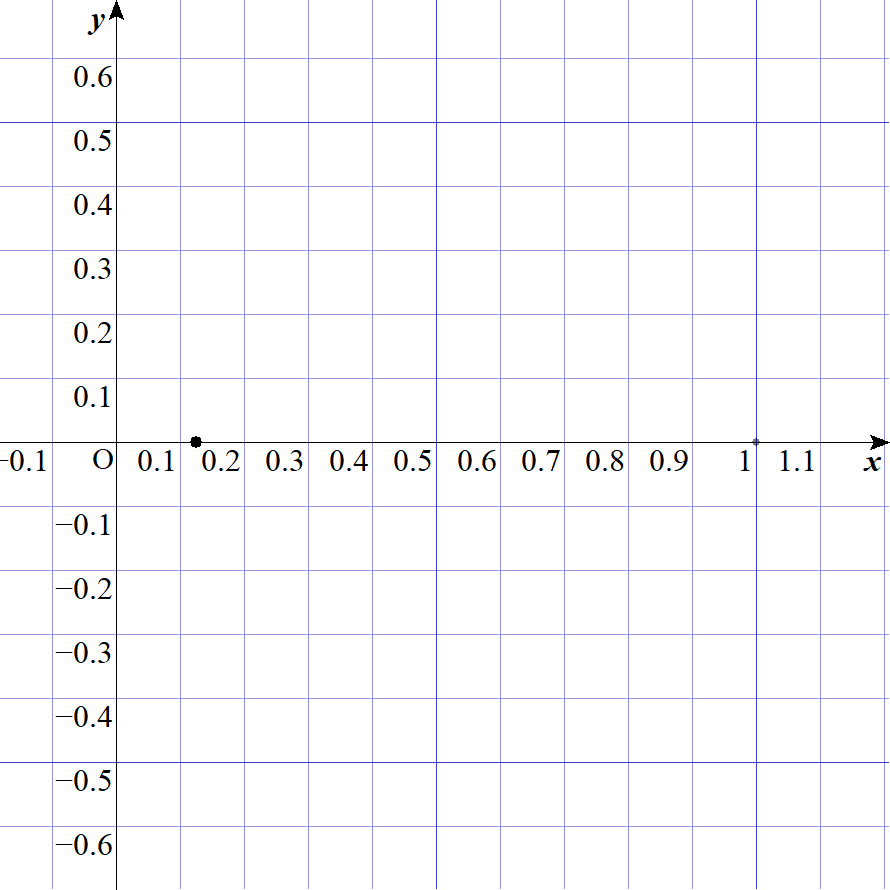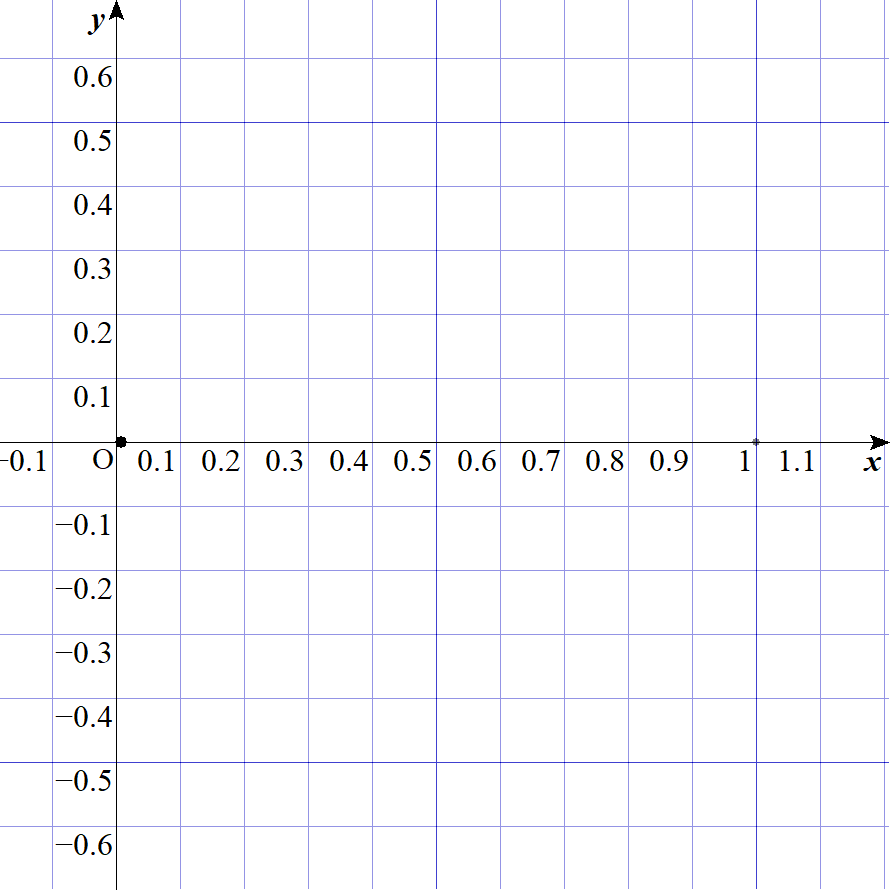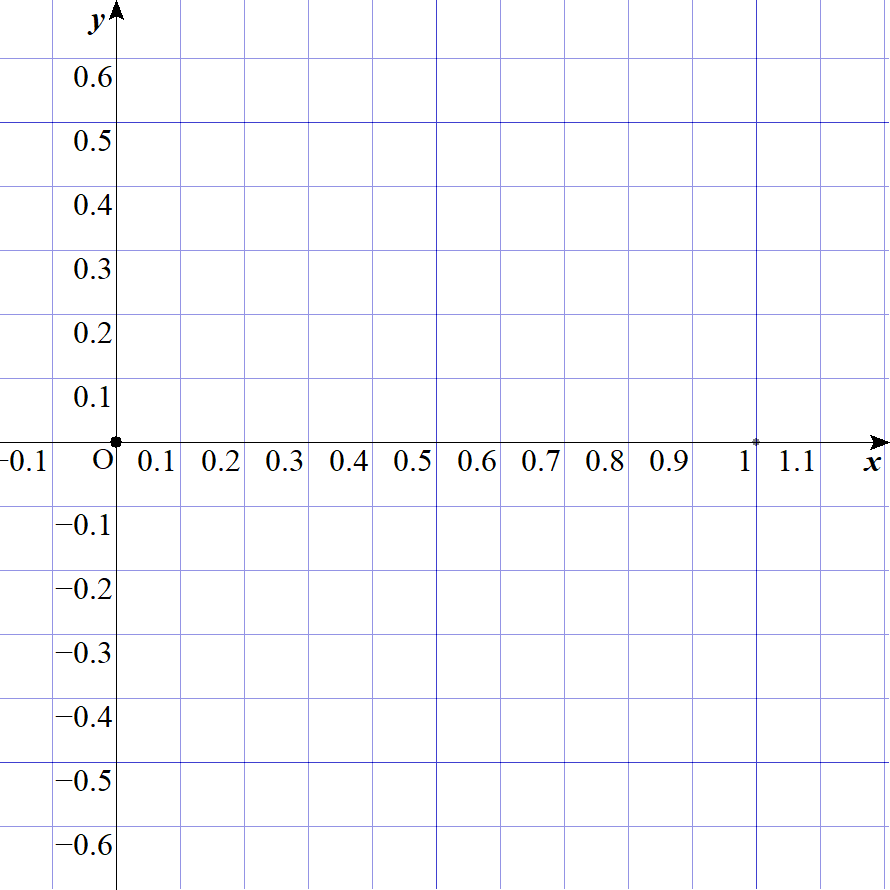
このgifは1,1/2,1/4,1/8,1/16,1/32,...と、分母を2倍していったときの点の移り変わりを示したものです。これをみれば、0に収束することが視覚的に分かります。 

このように、「限りなくこうなる」という極限特有の考え方を使うと、0.999...=1を適切に理解できます。

0.999...=1の意味

0.9

0.99

0.999

0.9999

...

0.9999999999999999999999

...

このように、小数点以下に9をつけ足していけば、その値は大きくなっていきます。9を付ければ付けただけ数はどんどん大きくなりますが、決して1は超えません。しかし、9をつけ足すことを際限なく繰り返していくと、その値は限りなく1に近づくのです。

0.9, 0.99, 0.999, ...と9をつけ足していくとある値に近づく。そこで、9を限りなく多くした状態を0.999...と書き、その限りなく近づく値こそが1であり、それを0.999...=1と書く。

これが結論です。世の中の0.999...≠1と言っている人に向かってこの言葉を突き付けてください。日常会話レベルならこの程度の説明で十分でしょう。

数学の用語を使えば、このようにも言えます。

0.9, 0.99, 0.999, ...という数列は1に収束する。

0.999...の一番の誤解？

1と2は違う数、1.0000023と1.0000022は違う数、というように、違う書き方をされたら違う数である、というのは当然の感覚で、それは間違っていません。

0.9999999999999999999と1は違う数です。これは9の個数に関係なく成り立つことで、たとえ小数点以下に9を9999億個ならべたとしても、9をいくつ増やしていっても1と等しくありません。これはれっきとした事実で正しいことです。しかしこれは0.999...=1が成り立たないという指摘にはなりえません。

間違った考え方

0.9≠1である。

0.99≠1である。

0.999≠1である。

...

0.99999999999999999999999999≠1である。

9をどこまで増やしていっても1と等しくなることはない。よって、

0.999...≠1

これの何がダメかというと、有限と無限の違いを無視しているのがダメです。

「よって、」の前に書いてある内容は、9が有限個なら1と等しくないという内容です。もちろんこれは正しです。しかし、いくら有限個で成り立つ例を持ってきたところで、9が「無限個並んでいる」0.999..が1と等しくないということは導けません。有限で成り立っていたから無限でも成り立つわけではないのです。

等比級数による証明

9をつけ足す、という表現が数学的にちゃんとしていないのが気になる人向け。
理系高校3年で習う等比級数というものがあります。このような公式があります。

 ここで、



と表されることを利用して、a=9/10, r=1/10を代入すると、

この等比級数の公式はもともと極限の考えを用いて導かれるものです。どちらにせよ、0.999...=1をしっかり説明しようとするとどうしても極限が必要になるのです。

このシリーズはここまで。無限小数は奥が深いのです。

written by k